
| 2010-10-25 07:29:45 |
Единица оказалась самой частой цифрой в научных данных
Первым "работу" закона заметил американский астроном Саймон Ньюкомб, в 1881 году обнаруживший, что в книгах с логарифмическими таблицами больше всего истрепаны страницы, где содержатся логарифмы чисел, начинающихся с единицы, и меньше всего - те, где приведены логарифмы чисел, начинающихся на 9. В 1938 году на этот факт обратил внимание физик Фрэнк Бенфорд, которому, в итоге удалось вывести уравнение, описывающее вероятность появления той или иной цифры в качестве первой значащей.
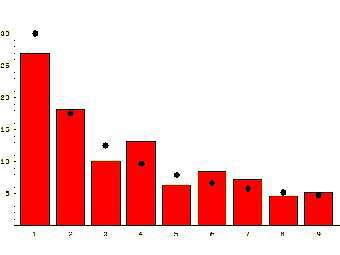
Согласно закону Бенфорда, единица встречается в подборках данных с частотой около 30,1 процента, двойка - 17,6 процента, тройка - 12,5 процента. Вероятность появления каждой следующей цифры падает, и у девятки она составляет только 4,6 процента.
Закон первой цифры справедлив для большого количества различных данных, в частности, для распределения длин рек, численности населения, высоты самых высоких зданий. Однако до сих пор все области данных, для которых закон Бенфорда выполняется, не определены.
Авторы новой работы проанализировали распределение первой значащей цифры в 15 наборах данных, содержащих, в общей сложности, 750 тысяч цифр. В исследовании были рассмотрены данные, полученные при изучении испускания протонов космическими объектами, выбросы парниковых газов в различных странах, количество людей-носителей тех или иных заболеваний и другие. Ученые установили, что все они подчиняются закону Бенфорда.
Исследователи полагают, что закон первой цифры благодаря своей универсальности может быть использован для получения новой информации об окружающем мире. В частности, с его помощью можно совершенствовать математические модели, которые описывают различные физические процессы. Кроме того, проверяя данные на соответствие закону Бенфорда, можно вычленять из случайного потока информации сведения о каких-либо неслучайных процессах. Так, по итогам анализа сейсмологических данных авторы смогли обнаружить, что в Австралии произошло небольшое землетрясение, не замеченное специалистами.
Некоторые коллеги авторов работы отнеслись к ее результатам несколько скептически. По мнению критиков, новое исследование всего лишь в очередной раз подтверждает, что закон Бенфорда работает для большого количества научных данных.
